Project Summary
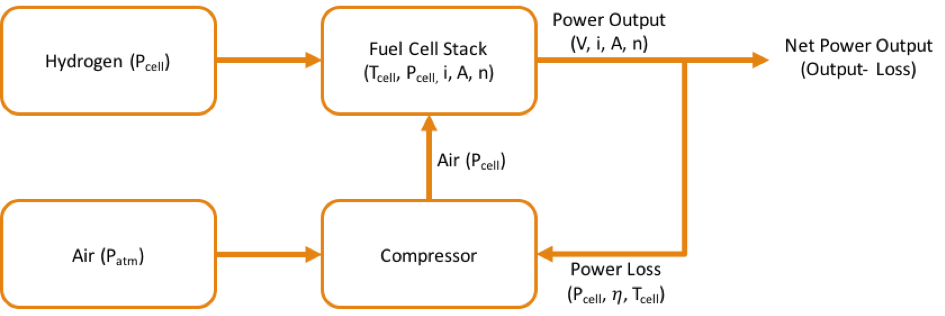
The output of the fuel cell depends on the current density (i), active surface area (A), and the voltage (V). Voltage is a function of pressure of the cell (Pcell), current density (i) and active area (A). More the pressure, more is the voltage and hence, more is the power output. However, for the system to run at a higher pressure, the compression ratio has to be high, as a result of which the the compressor draws more power from the fuel cell system, which decreases the net power output of the fuel cell.
Summary
The objective of this optimization is to find out the optimum pressure the system must be run at, such that there is maximum power output with minimum power loss Maximize: Net Power=Power Output-Power Loss
Results
Base Case: compressor with 60% efficiency
Case 1: compressor with 30% efficiency
Case 2: compressor with 90% efficiency
| Variable | 60% Efficiency (Base Case) | 30% efficiency | 90% Efficiency |
|---|---|---|---|
| Current Density (A/cm2) | 0.38 | 0.379 | 0.39 |
| Pressure (atm) | 1.51 | 1.00 | 2.85 |
| Temperature (K) | 362.63 | 357.90 | 370.83 |
| Power (W) | 376.32 | 372.11 | 391.99 |
Power output decreases with decrease in in efficiency of the compressor. At 30% efficiency the compressor draws more power than it would add. Hence, the optimum solution is to run the system with no compression.
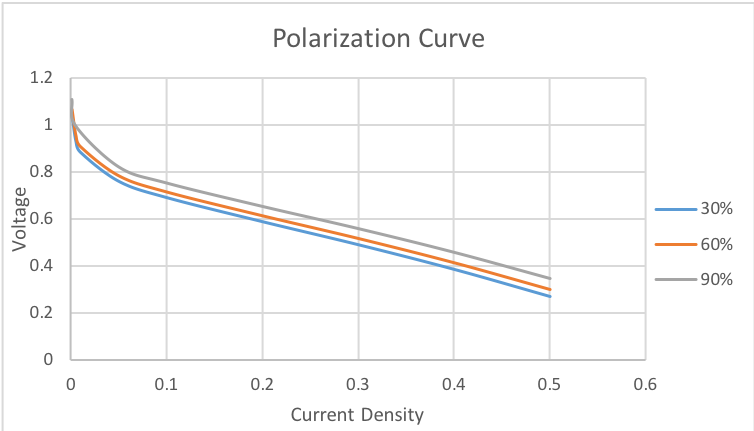
With increase in efficiency the polarization curve shifts upward and hence more voltage is obtained for the same current density which increases the power output.
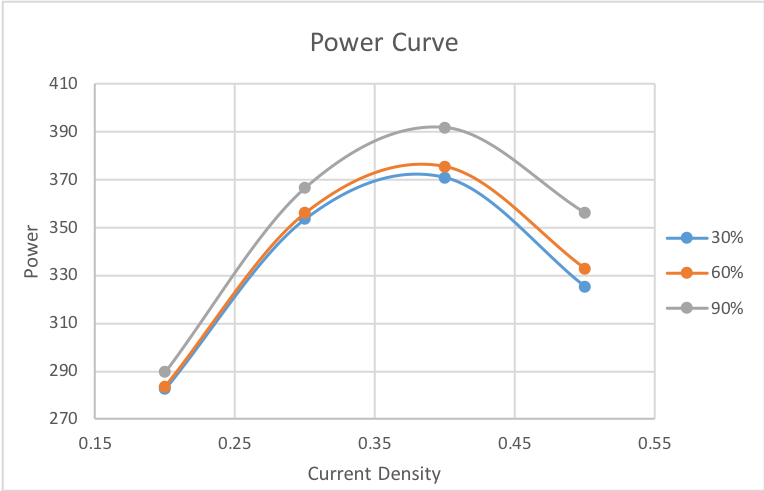
The power curve shifts upward with increase in efficiency because of higher voltage.
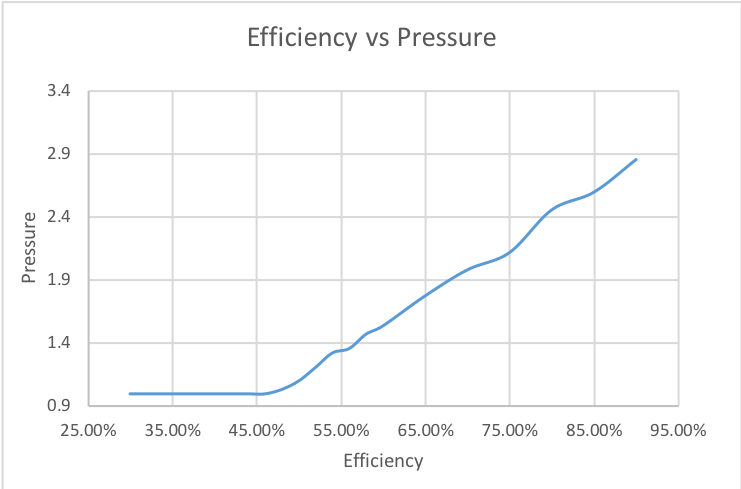
The above plot of efficiency vs optimum pressure shows that, only when the efficiency of the compressor is above around 48% it makes sense to have a compressor. This is because below 48% efficiency the compressor draws more power than it adds to the power output of the fuel cell.